导数

导数
初渝一、导数定义
导数定义的几种等价形式: 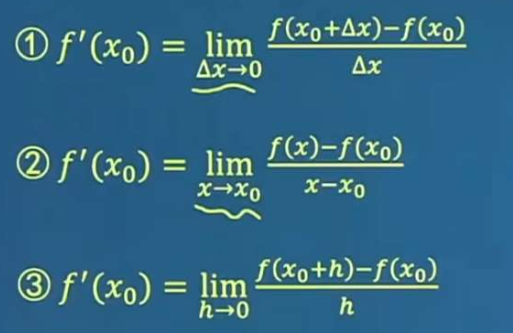 2个小总结:
2个小总结: 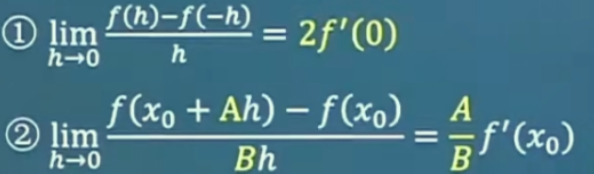 <<<<<<<
HEAD
<<<<<<<
HEAD
二、可导与连续的关系
可导必连续,连续不一定可导,不连续一定不可导
三、基本导数公式
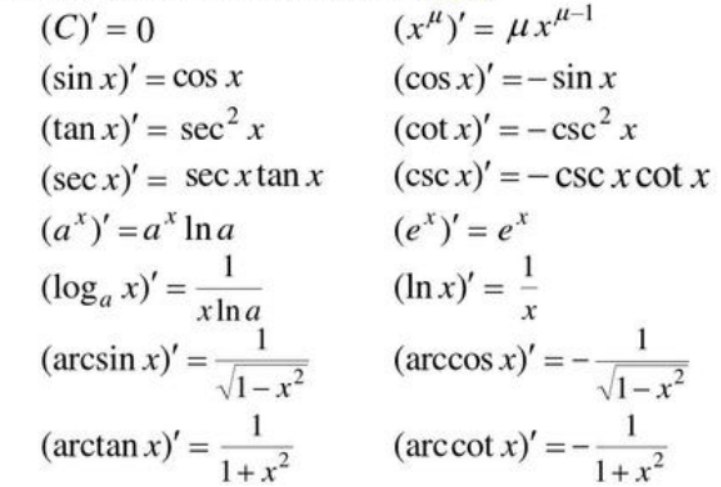
四、求导法则:

五、反函数求导
反函数求导法则:反函数的导数等于原函数导数的倒数
六、复合函数求导
复合函数求导法则:先外层求导,再乘内层求导
七、分段函数求导
方法:分段点两边分别求,中间分段点单独求
八、隐函数求导
方法:方程两边分别求导,注意方程中y是x的复合函数
=======
二、可导与连续的关系
可导必连续,连续不一定可导,不连续一定不可导
三、基本导数公式
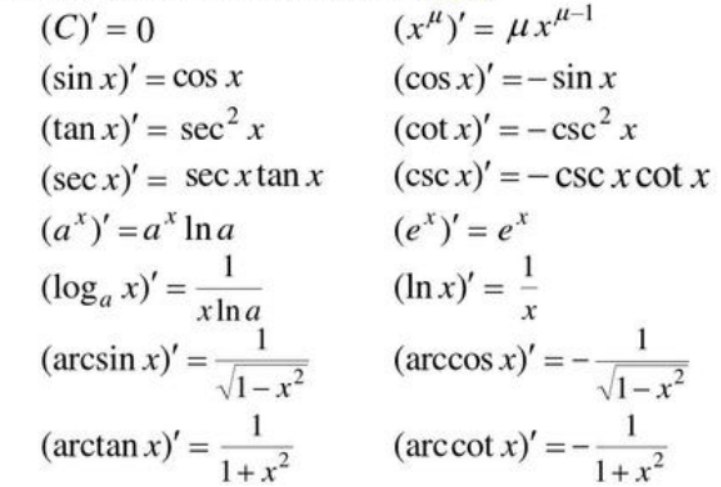
四、求导法则:

五、反函数求导
反函数求导法则:反函数的导数等于原函数导数的倒数
六、复合函数求导
复合函数求导法则:先外层求导,再乘内层求导
七、分段函数求导
方法:分段点两边分别求,中间分段点单独求
八、隐函数求导
方法:方程两边分别求导,注意方程中y是x的复合函数
c402237 (由 git bash 自动提交)
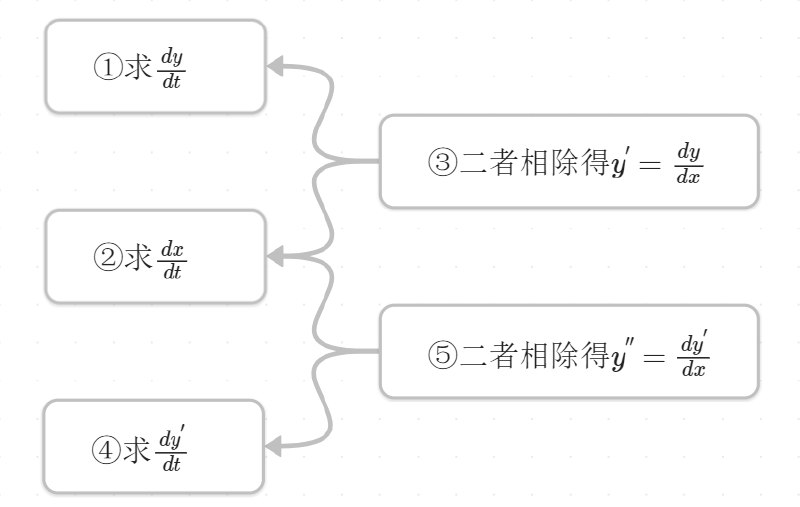
九、由参数方程确定的函数求导
方法:y对t的导数除以x对t的导数
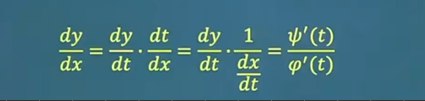
十、幂指函数求导
方法:对数求导法
十一、多因子积商乘方构成的函数求导
方法:对数求导法
对于多因子积商乘方构成的函数,也可以先对函数两边同时取对数,化积商为加减,化乘方开方为系数,然后再根据复合函数的求导法则进行
十二、高阶导数
(一)高阶导数的定义
对函数y=f(x)求导得到的
对
对
对
(二)求高阶导数的方法
情况1: 求二阶或三阶导数
方法:先求一阶导,再求二阶、三阶导
情况2:求三阶以上的导数
方法:建议使用“常用”高阶求导公式 
(三)求由参数方程确定的函数的二阶导数