微分

微分
初渝一、基本微分公式及运算法则

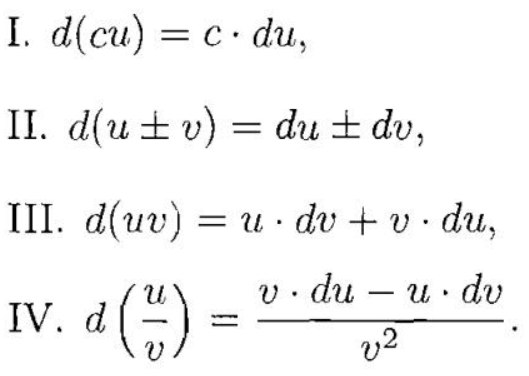
二、微分中值定理
(一)罗尔中值定理
如果函数
满足下列三个条件:
(1)在闭区间[a,b]上连续;
(2)在开区间(a,b)内可导;
(3),
则在开区间(a,b)内至少存在一点,使得
题型1:证明方程在开区间内有实根
若函数
解题思路:
- 第一步:构造导函数
- 第二步:根据
求函数 - 利用求导法则的反向运算;
- 第三步:将两端点代入
- 若二者相等,则根据罗尔定理得以证明
构造函数
显然
所以
解题思路:
- 第一步:构造导函数
- 第二步:根据
求函数 - 利用求导法则的反向运算;
- 第三步:将两端点代入
- 若二者相等,则根据罗尔定理得以证明
构造函数
显然
所以
(二)拉格朗日中值定理
如果函数
满足下列两个条件:
(1)在闭区间[a,b]上连续;
(2)在开区间内可导;
则在开区间内至少存在一点,使得
题型2:证明双边不等式
显然
所以
因为




